诚然网格画到无穷小，刚度矩阵无穷大，但这样没法计算，那网格画到什么层度精度最高？

　　众所周知，网格是有限元分析非常重要的一部分，结构离散后的网格质量直接影响到求解时间及求解结果的正确性,那网格画到什么层度精度最高？

　　元王小编认为在单元选用合理、计算假设合理、网格划分合理的前提下，单元数量越多，结果越接近理论解。

　　很多时候，提高单元数量对于计算精度的提高，远远比不过选用更好更合理的单元类型。对于不同的求算对象，所需要的单元数量也不相同。一般来说，求算应力需要比求算位移更多的单元，而求算剪应力需要比正应力更多的单元。

　　举一个常见小例子，平面应力问题，计算一根悬臂梁的变形和应力：

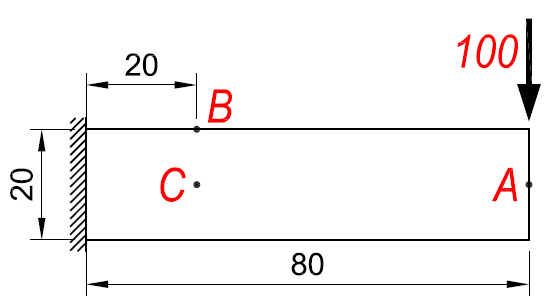
　　悬臂梁的宽度为1，弹性模量30000，泊松比0.3，自由端承受竖向荷载100。求解A点的竖向位移、B点的正应力、C点的剪应力。

　　分别选用不同类型的四种单元计算，包括三节点三角形 CSTG、六节点三角形 LST、四节点四边形 IPLQ、八节点四边形 IPQQ。

　　首先计算位移和应力的理论解：

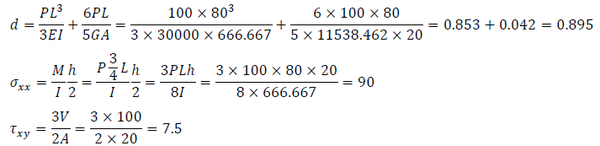
　　A 点的竖向位移为0.895，B 点的正应力为90，C 点的剪应力为7.5。

　　然后分别用不同数量的四种单元进行比较计算，所用软件为 GT STRUDL，单元名称按照 GT STRUDL 的命名，计算结果是这样的：

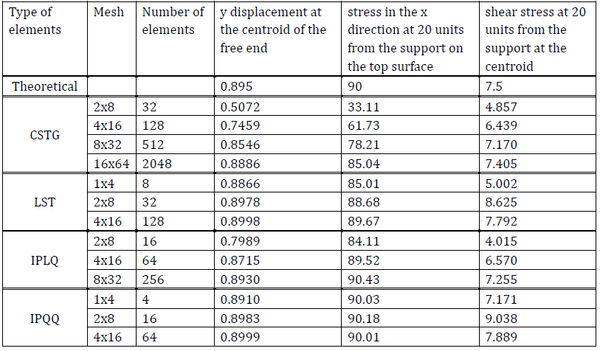
　　随着单元数量的增多，位移、正应力和剪应力结果都趋近于理论解。

　　对于不同的单元类型，趋近理论解的速度完全不同。同样是32个单元，CSTG 的位移结果是0.5072，正应力是33.11，与真实解 0.895 和 90 相差甚远。而32个单元的 LST 结果为0.8978和88.68，已经很接近于理论解 0.895 和 90。

　　同样是64个单元，IPLQ 的结果为 0.8715 、89.52，而 IPQQ 的结果则达到了 0.8999、90.01，可以说正应力结果已经非常非常接近理论解。

　　如果比较一下四边形单元的结果和三角形单元的结果，差异更加明显。对于位移结果来说，2000个CSTG单元的精度也比不上4个IPQQ单元的精度。

　　如果横坐标为单元数量，纵坐标为计算结果，绘制一张收敛图像的话，对于位移来说是这样的：

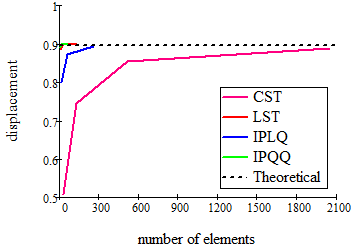
对于这四种单元类型，要想达到类似的可以接受的精度水平，需要的单元数量完全不同。

　　根据上面的分析，想要得到精度可以接受的计算结果，CSTG 需要2000多个单元，而 IPQQ 仅需要64个。

　　所以结论就是，提高单元数量的确会提高计算精度，但前提是单元类型合理高效。对于提高精度来说，更合理的方法是选用更好的单元，而不是盲目的提高单元数量。

　　Abaqus 的结果如下：

　　不同单元在四种网格尺寸（1x6、2x12、4x12、8x24）下的计算结果与理论解的比值

CPS4：0.074，0.242，0.242，0.561
CPS8：0.994，1.000，1.000，1.000
CPS4R：20，1.308，1.051，1.012
CPS8R：1.000，1.000，1.000，1.000